*Update 2023-03-17: Our in-depth analysis is now available here.
Update 2023-03-07: Since publishing this article, we have been studying the object much more closely, and have managed to recreate a mathematical model representing many of the overall design configurations and methodologies of the object. From this, we have reached a number of new and interesting insights. As a consequence, we have also revised and updated some of the initial measurements made in this article.
This article will not be corrected or updated, as it reflects what our best understanding of the object was, at the time of publishing this, and documents what initial observations led to the discovery of a more suitable overall model. We have, however, added a few "Notes from the future" where relevant, that points out how our initial observations deviated from the model we are working with now.
Have a look at this update demonstrating how Pi was integrated to near perfection into the design as well.
We are compiling all of our findings and current understanding into a new set of articles, and will be releasing them in the near future.
An extremely accurate and high-resolution mesh, obtained via structured-light scanning, has just recently been released of vase-like object, that is purpoted to originate from pre-dynastic Egypt. This would, if true, mean that the artifact was produced over 5000 years ago, which is quite a remarkable claim, given some of its properties. The ratios and angles used in the construction of the object tells an interesting story, and reveals some intruiging points about its design and creation.
Since this is a rather long and laborious article, I will start out with a little teaser, so you can make sure that it's worth your time. Due to its specific design configuration, there is less than a 1 in 10²⁰ chance that it simply "randomly appeared" like this. To create an object with this kind of configuration, it would have to be very carefully designed. You could cover the surface of the entire Earth with random permutations of this vase, and not one of them would be a configuration so perfect and exact as this one.

When I first heard about this object, I was quite intrigued by the claimed uniformity and extreme tolerances to which it was manufactured. If you haven't seen it, you can get an overview of the object in this video. A Polyworks report was released by Alex Dunn and Nick Sierra on the UnchartedX website.
I am in absolutely no position to judge the real age of the object, but even if it was made yesterday, and the maker had access to modern CNC machinery, it is a entirely marvelous job of manufacturing. Assuming that the claimed precision and uniformity are in fact true, I'm not even sure anyone in our modern age would have been able to make something like that at all, to such a high level of precision, until very recently.
Marián Marčiš, who specialises in photogrammetry and laser scanning of cultural heritage, has also been looking at some of the interesting properties of the object:
I have made some initial observations and geometric analysis relating to the object, that I'd like to share. Some of the things that have come to light here are really quite remarkable. I will hold off on connecting the dots between the different findings, and leave the drawing of certain conclusions to the reader. For now, at least.
In this early analysis, I have not given any weight to absolute measurements, since such are completely irrelevant to an analysis like this. Whoever might have made this object might not have used the same measurement standards as us, so at this point, only the relations can have any meaning to us here. That being said, any absolute measures given are in millimeters.
A very interesting future line of work might be to figure out what units of measure was actually used though, and given the highly geometrically and mathematically consistent nature of the object, this might actually be a possibility.
It also bears note, that I am of course not interacting with the granite artifact itself, but a (very good, I dare say) digital representation, I will still just refer to it as the object from here on in this article. In many ways, this scan is better than pondering the object only by physical sight and touch.
Of course, I absolutely wouldn't pass down the chance to see it with my own eyes!
Already during my initial observations, it was clear that this was quite a remarkable object. The extreme uniformity and precision of it's constituent shapes is totally unlike anything I've seen outside of precision machine shops. Being able to directly interact with this digital copy holds great value, and I am very grateful towards the team at UnchartedX for making it freely available to the world.
The tolerances this object was manufactured within are mind-boggling. I have access to, and regularly use, a high-end CNC-controlled laser cutter, and I would not have been able to create so borderline perfect a curvature with it, in acrylic. This object was made from granite.
At first glance it stood out to me as a sort of show-piece, that somebody would make to demonstrate, beyond a shadow of a doubt, that they were masterfully skilled craftsmen. But the more I looked at it and thought about its various features and properties, the more it boggled my mind. I've seen a lot of really fancy stuff made on really fancy 5-axis machines, but in many ways, this object is more impressive.
I will move onto the more technical analysis now, but I feel it important to stress, that this object really is quite remarkable in the methods that must have been used to produce it. Whoever made it, and whenever it was done, the result tell a story that has, quite literally, been written in stone.
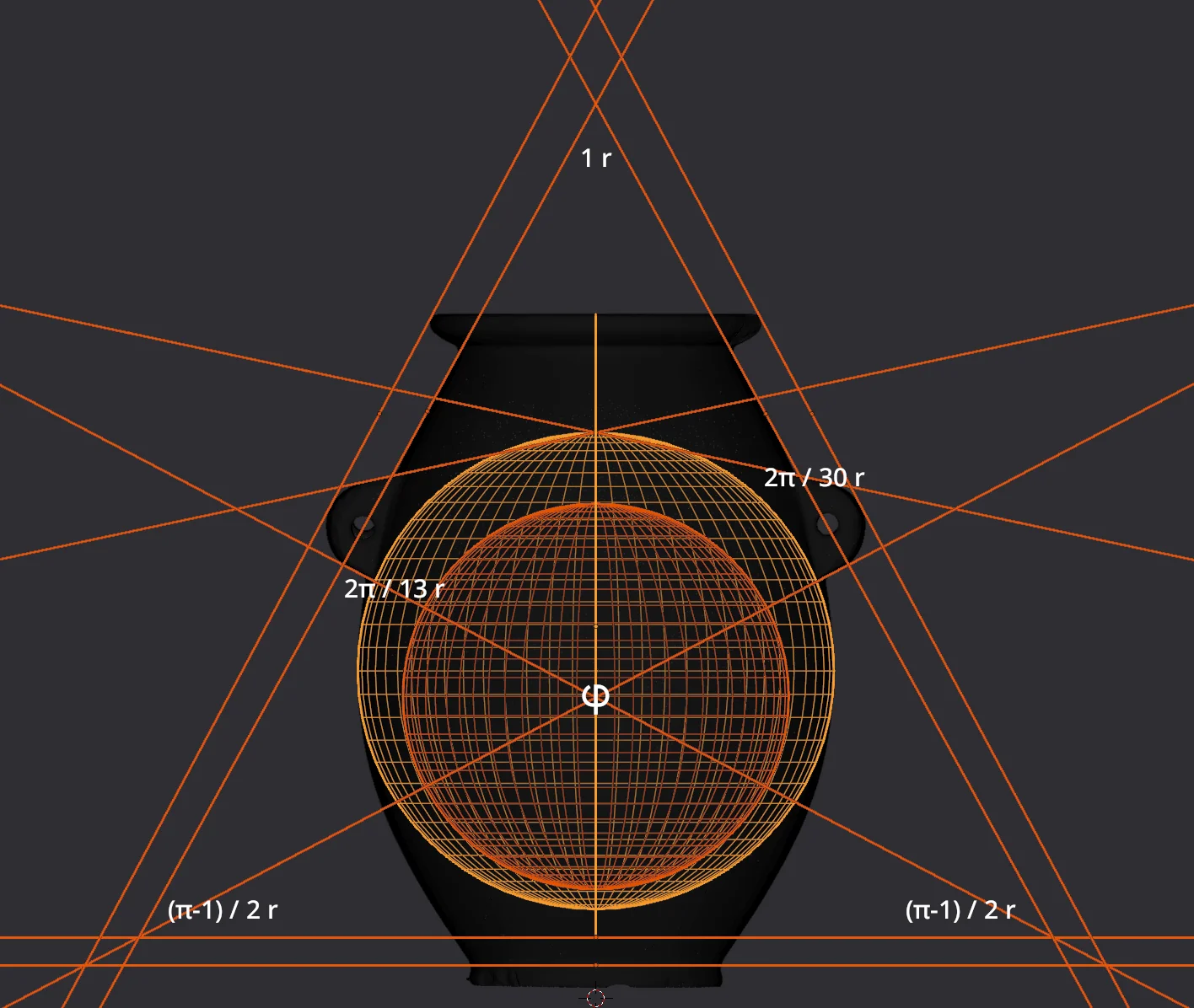
From the initial external observations, it is clear that we are dealing with an ellipsoid object. An equation describing the complete curvature of the object is not immediately obvious, but it turns out we can at least create two spheres that help define it.
We will define one sphere that is precisely tangent to the maximal external circumference of the ellipsoid (barring the handles, which we shall get to). Let's call it the external sphere:

We will define another sphere, that is precisely tangent to the maximal internal circumference of the internal cavity of the object. Let's call it the internal sphere:

These two spheres were aligned as precisely as possible with the scanned mesh vertices, which corresponds to less than 0.05 millimeters. Alone, these two spheres don't tell us much, but one very curious property of them is the ratio of their radii, which, to the best precision I can measure here, is approximately $1.23$. Not much of a lead for anything, but really quite odd and interesting.
Note from the future: This is not the exact ratio - our initial measurement here was off by around 0.4%.
The handles on the vase are incredibly interesting features, and I will have to restrain myself not to write an entire book on the subject. For this purpose I shall try to concern myself exclusively with their geometric properties.
Others have described them as cylinders, which I will have to disagree with. They are in fact sections of a toroid, and incredibly precise ones, at that.
An interesting avenue I haven't explored yet, is that the right handle (in this setup) seems to have been damaged, or had some material removed at some point, and that the toroid segment making up the left handle is slightly rotated around the center-axis of the object.
We can easily model the handles as a section of a toroid wrapping the entire circumference of the object:

Here is a closeup from above:

It is absolutely astounding how closely most of the handles match a spherically based toroid. One very interesting feature though, is that they have parts not matching the base-sphere of the toroid. On these parts of the handles, there are relatively short, but linear segments connecting the toroid to the main body of the object:

Now... I wonder what happens if we extend those linear segments...
When I did this extension, I have to admit I was quite astonished. Extending the linear segments of the upper part of the handles creates two lines, that intersect exactly at the apex of the external sphere:
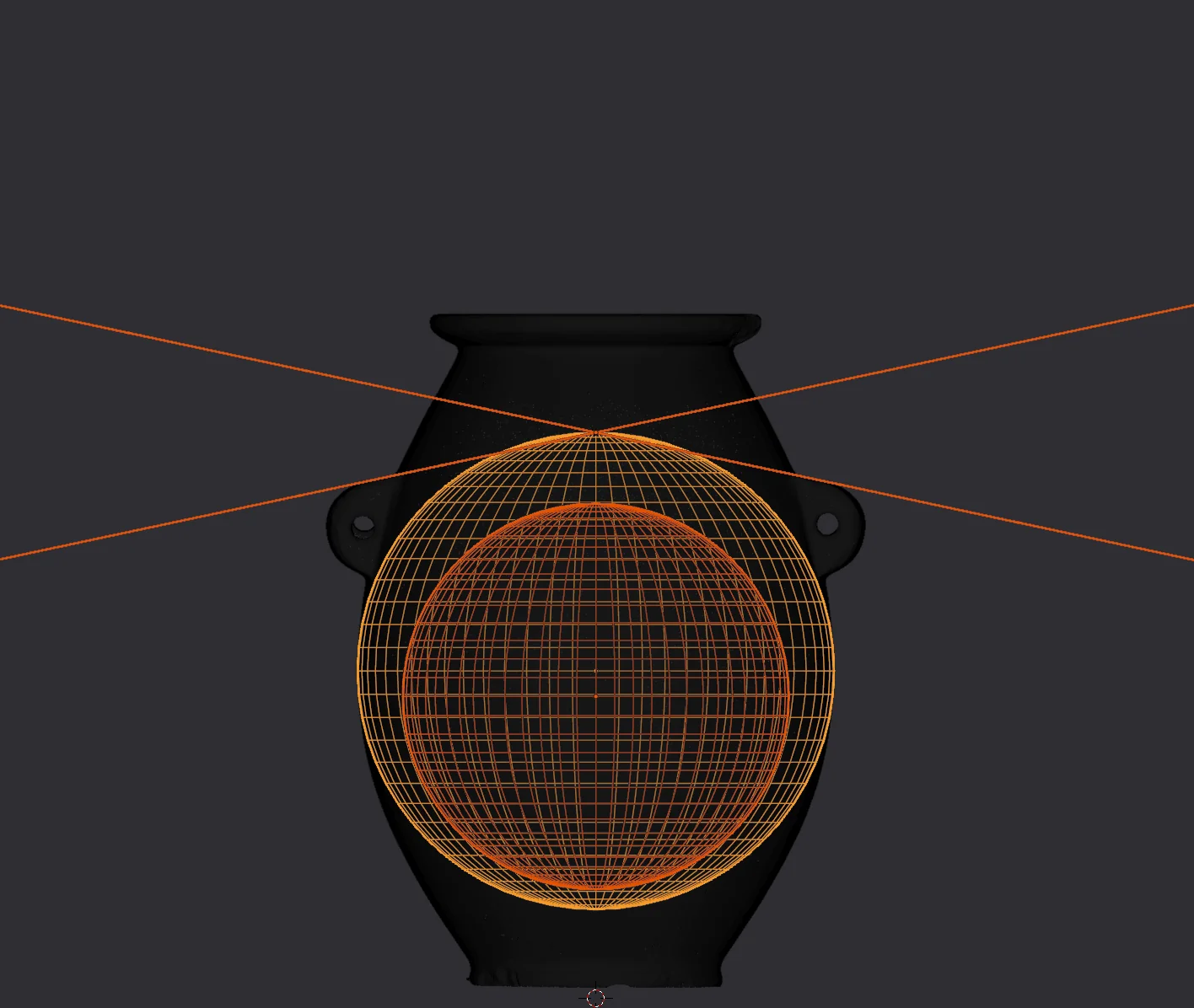
Likewise, extending the linear segments of the lower parts of the handles creates lines that intersect at the exact center point of the internal sphere.
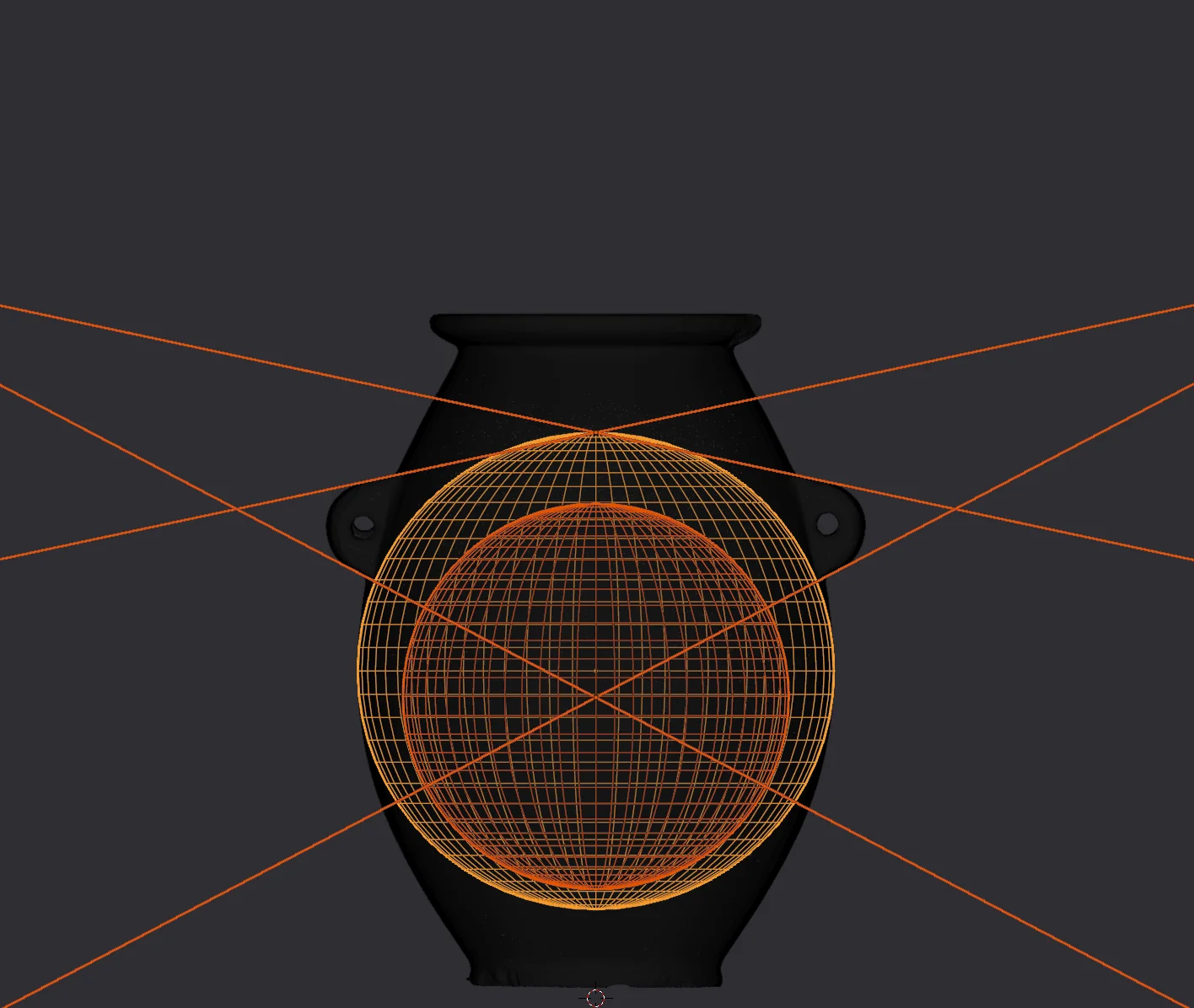
Of further notice is the fact, that the angle of the upper line segments in relation to the datum plane defined by the top of the object is exactly $2π \over 30$ radians. Likewise, the angle of the lower line segments is exactly $2π \over 13$ radians.
Note from the future: These angular measurements were pretty close, but have been revised in our updated model, that integrates much better with the rest of the object.
These facts, even isolated and in their own right, represent some pretty deliberate (and very beautiful) design work.
After seeing the above, I started looking for more linear segments, of which there are not really a whole bunch, in an object made by someone who obviously loved curvature. But at least a few more do exist.
It's not immediately obvious, but part of the upper main body is actually a cone segment without any curvature. Taking the angle of this segment, we can project the following lines:

Before moving on, I want to note the interesting feature, that these lines seem to pass through the center-points of the holes in the handles. But it looks like something has been done to those at some point, and that they are no longer in their original shape. Or maybe there is more interesting geometry hidden in their irregularities? I haven't analysed them yet.
By carrying out the line projections, we immediately see something quite interesting starting to emerge. Let's add the last part of the triangle formed by the intersection with the previous line segment projections:

If my eyes don't deceive me, that's an equilateral triangle. But no, they actually do deceive me! Measuring it tells us a slightly different story, and this is one that is actually a lot more interesting:
As good as I can measure it here, the angle of the top is exactly $1$ radian. The other two is then of course approximately $1.0708$ radians, or to be more exact: $π-1 \over 2$. It's... I'm trying to keep a straight face here. But just, wow. It's like someone was trying to make a pretty strong point here.
One could make some rather profound conclusions, regarding the capacity of the objects makers for precision in numerical calculations, to be able to pull this off. But I am going to resist that temptation for now, and return to the subject at hand. Let's suffice draw the readers attention towards the fact, that as far as we currently know, nobody on earth had an algorithmic method to calculate arbitrary decimal points of π before somewhere around 250 BC. Additionally, the first true sine and cosine tables does not appear until some 750 years later, made by Hindu mathematicians around 500 AD.
Incidentially, I actually think that the bottom side of this triangle coincides with where the original floor was inside it, at some point in its history. If you inspect the inside of it, you will see that the inside floor of the cavity is, compared to the rest of the object, uncharacteristically uneven. It looks very much like it has been damaged, worn or altered over time. At the very least, we can assume this line as a design plane of the internal cavity.
Note from the future: In retrospect, the assumption that the interior floor should have been worn or damaged, does not seem like a very solid explanation for why the actual floor would deviate from the geometrical plane defined by the intersections.
If we add a bisection to the geometry, and trace it upwards until we see the uneven features disappear along the wall, this location coincides with the plane marked by the bottom part of the triangle. This may or may not turn out to be incorrect, but for the sake of this initial analysis, I will make the assumption that the floor of the internal cavity was originally coincident with the bottom part of the triangle.
Right, so at this point I was honestly almost expecting it, and sure enough. Using the newfound original floor of the internal cavity, we can now calculate the ratio between the total depth of the cavity, and its maximum diameter:
Well, at least it is equals $φ$ to within tolerances I am most comfortable calling good enough.

I honestly think this is quite profound. Whoever made this object had a deep understanding of mathematics and geometry. At this point I am going to say that there is absolutely no way this object could just have been made. It was very, very carefully designed and fabricated.
The golden ratio actually appears at least one more time in the object, and with a little observation, you should be able to spot it quite easily in the first image of this article. Here again, it is present to absolutely stunning precision, with deviations from perfect at around 0.05 millimeters.
There are also some very strong indications here, that hint at what kind of methods and tools the object was designed with, but I promised not to draw too many conclusions here, so I will wait with that, at least for now.
After viewing the inner triangle formed by the previous line projections, it's actually rather clear that another such exist. By creating lines that are tangent with both the lip of the object and the handles, we are treated with another triangle that is almost identical in composition to the inner one:

An interesting feature of this triangle is that the length of the bottom segment is exactly two times the diameter of the outer sphere, or the maximum diameter of the toroid, in other words.
This initial geometric analysis, of this fascinating object has been extremely interesting, and quite surprising, to put it mildly. As an initial exploration, I think this overview will suffice, but I will definitely be studying the object more closely. Carrying out this excercise has certainly provided ample food for thought.
I've already discovered a few more interesting features, that I didn't have time to add graphics of here, like the radial completion of the $2π \over 13$ pattern from the handle projection, that maps to at least one other feature of the object. And just from a glance at the above diagram, several new obvious avenues of exploration immediately stand out.
I have a feeling there's a lot more interesting things to discover here. One thing is quite clear to me at this point though: This object much more closely resembles a mathematical map, than it does a vase.


